An Introduction To The p-adic Numbers
Intro
"... in mathematics you don't understand things. You just get used to them"- John Von Neumann
I wanted to write a simple introduction to the p-adic numbers, however in my research I came across this youtube video, which does a better job than I ever could have.
I had started writing this up and had most of the same ideas in place before finding this video, however I found the structure and approach of this video to be exemplary. I restructured what I had to be in roughly the same order and I found that the content was almost identical.
I decided to continue writing this even though there is already an excellent resource on this in order to practice my technical writing a little.
In any case, all credit to the merits of this post should go to the video's creator Rokker815, while any defects are surely my own.
I am going to walk you through a simplified construction of the p-adic numbers by showing the similarities to how the reals are constructed. Then we will go through some properties of the p-adic numbers.
This post is structured in the following order:
- Tools
- p-adic Absolute Value and Metric
- Geometry of \(( \mathbb{Q}, d_p )\)
- Motivation for \( \mathbb{Q}_p \)
- Properties of \( \mathbb{Q}_p \)
Tools
First, some definitions:
Rational Numbers: \(\mathbb{Q} = \{ \frac{a}{b} | a, b \in \mathbb{Z}, b \ne 0 \}\)
Field: a set \( \mathbb{F} \) on which \( +, -, \times, \div \) are defined and behave as expected (e.g. \(\mathbb{Q}\) with normal operations forms a field, but \(\mathbb{N}\) with normal operations is NOT a field)
Absolute Value: First define \( \mathbb{Q}_{\geq 0} = \{ x \in \mathbb{Q} | x \geq 0\}\) (known as the nonnegative rationals). Then any function \( | \cdot | : \mathbb{F} \rightarrow \mathbb{Q}_{\geq 0}\) that satisfies
- \(|a| \geq 0\)
- \(|a| = 0 \iff a = 0\)
- \(|ab| = |a||b|\)
- \(|a + b| \leq |a| + |b|\)
is known as an absolute value on the field (absolute values are not unique. For example there is always the trivial one where it takes value 0 for some value of \(\mathbb{F}\) and 1 for all other values).
The classic absolute value on \(\mathbb{Q}\) is that \(|x|\) is just \(x\) when \(x \in \mathbb{Q}_{\geq 0}\) and \(-x\) otherwise.
Metric Space: given a set \(X\), a metric \(d\), is a "distance" function \(d: X \times X \rightarrow \mathbb{Q}_+\) which has the following properties:
- \(d(x,y) \geq 0\)
- \(d(x,y) = 0 \iff x = y\)
- \(d(x,y) = d(y,x)\)
- \(d(x,y) \leq d(x,z) + d(y,z)\)
A metric space is a set \(X\), with a metric on it \((X, d)\).
e.g. a set \(\mathbb{Q}\), and a metric \(d(x,y) = |x - y|\), give us a metric space \((\mathbb{Q}, d)\).
Open Ball: \(B(a, r) = \{x \in X | d(a, x) < r\}\)
e.g.
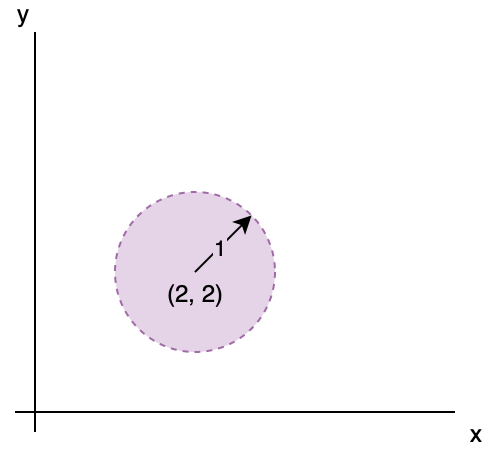
One Way to Express a Rational Number
Fix \(p\) prime. Let \(x \in \mathbb{Q}\). The we can always express \(x\) as
\(x = p^ n \frac{g}{h}\)
where \(\frac{g}{h}\) is a fraction in its lowest terms (i.e. neither \(g\) or \(h\) is divisible by \(p\).)
p-adic Absolute Value on Q
For \(x\in\mathbb{Q}, x \neq 0\) we define the p-adic absolute value from the rationals to the non-negative rationals as \(|\cdot|_p : \mathbb{Q} \rightarrow \mathbb{Q}_+\), as \(|x|_p = |p^n\frac{g}{h}| = p^{-n}\) and \(|0|_p = 0\)
e.g.let \(p=7, x = \frac{147}{5}\) then you have \(|\frac{147}{5}|_7 = |7^2\frac{3}{5}|_7 = 7^{-2}\)
p-adic metric on Q
\(d_p : \mathbb{Q} \times \mathbb{Q} \rightarrow \mathbb{Q}_{\geq 0}\)
\(d_p(x,y) : {| x - y |}_p\)
e.g. for \(p=5\) we claim that 627 and 2 are closer together than 3 and 2. \(d_5(657, 2) = |625|_5 = |5^3|_5 = 5^{-3}|\) and \(d_5(3,2) = |1|_5 = |5^0| = 1\).
Geometry of Open Balls
Consider \((\mathbb{Q}, d_p)\). Then \(B(a,r) = \{x \in \mathbb{Q}: d(a,x) < r\}\). By the definition of \(| \cdot |_p\ r\) will only take discrete values in \(\{p^n, n\in\mathbb{Z}\}\). This gives a very interesting geometric intepretation.
e.g.
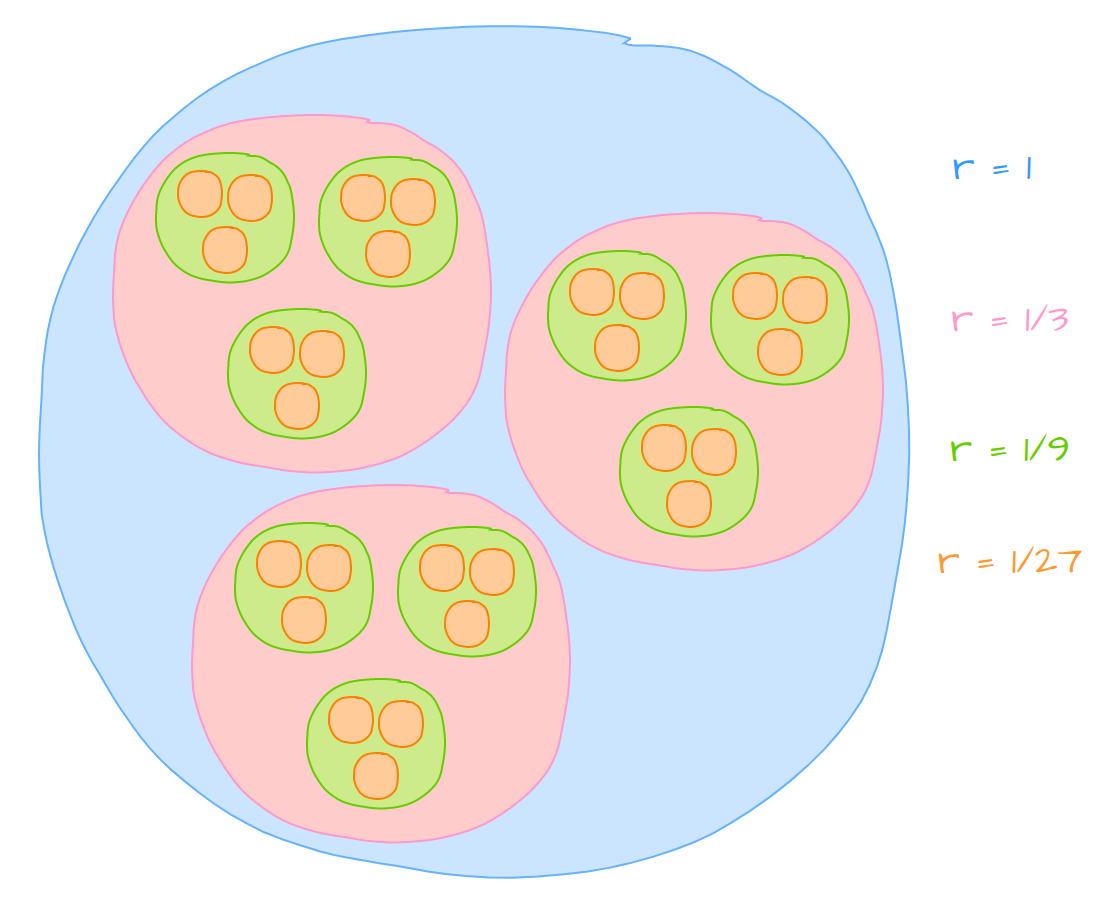
Cauchy Sequences
Let \( (X, d) \) be a metric space.
Formally, a sequence \((x_1, x_2, x_3, x_4, ...) \in X\) is called a Cauchy Sequence if for every real number \(\varepsilon\) there exists an \(N \in \mathbb{N}\) such that for every \(m,n > N\) you have \( d(x_m, x_n) < \varepsilon \)
Cauchy sequences allow us to use words like "eventually" and "arbitrarily" in a formal sense.
Completeness
A metric space \( (X, d) \) is complete if every Cauchy Sequence converges.
e.g. \(( \mathbb{Q}, d )\) is NOT complete because the sequence \( (1, 1.4, 1.41, 1.414, 1.4142, ...) \) gets arbitrarily close to \(\sqrt{2}\) - that is, it forms a Cauchy Sequence, but it does not converge in \(\mathbb{Q}\) as \( \sqrt{2} \notin \mathbb{Q}\)
Construction Of The Reals
As we've seen, the rationals have Cauchy sequences that do not converge. What would happen if we were to "plug" these "missing" values? What we'd in fact be doing is "completing" the rationals with respect to it's metric. When you complete a field, it turns out that you get another field. When you complete the rationals with respect to the regular absolute value metric, what we get is the reals! i.e. the completion of \((\mathbb{Q}, d) = \mathbb{R}\)
Is \((\mathbb{Q}, d_p)\) Complete?
No. Why?
Fix \(p=3\), i.e. we are considering \((\mathbb{Q}, d_3)\)
Consider the sum \(1 + 3 + 3^2 + 3^3 + \dots \notin \mathbb{Q}\)
Now consider the sequence of partial sums
\(\{1, 1+3, 1+ 3+3^2, 1+3+3^3+3^3, \dots\} = \{1, 4, 13, 40, \dots\}\)
This sequence is Cauchy with respect to \(d_3\)
So since we have a Cauchy sequence that does not converge, \((\mathbb{Q}, d_3)\) is not complete. A similar construction can be made for each \((\mathbb{Q}, d_p)\).
Completion of \((\mathbb{Q}, d_p)\)
\(\mathbb{Q}_p =\) the completion of \((\mathbb{Q}, d_p)\)
Every p-adic number (\(x \in \mathbb{Q}_p\)) can be written as:
\(x = \dots + a_kp^k + a_{k-1}p^{k-1} + \dots + a_0 + \dots + a_{-k + 1}p^{-k + 1} + a_{-k}p^{-k} + \dots \)
Which can be written more conveniently as:
\(x = \overline{(\dots a_ka_{k-1}\dots a_0\dots a_{-k+1}a_{-k}\dots)_{\mathbb{Q}_p}}\)
Properties of \( \mathbb{Q}_p \)
\(\sum_{n=0}^\infty (p-1)p^n = -1\)
All triangles in \(\mathbb{Q}_p\) are isosceles
\(\mathbb{Q}_p\) is not ordered
\(\mathbb{Q}_p\) is not comparable with \(\mathbb{R}\)
\(x^2 = -1\) has a solution \(x \ \mathbb{Q}_p \iff p = 1 \) mod(4)
Bibliography
- Youtube: Introduction to p-adic Numbers*
- Youtube: What does it feel like to invent math?
- Ostrowski's theorem
- What are p-Adic Numbers? What are They Used for?
- p-adic Number
- The p-adic topologies on \(\mathbb{Q}\)
- The p-adic Numbers
- p-adic integer
- A Tutorial on p-adic Arithmetic
- p-adic Number
- p-ADIC NUMBERS
* - this post is at best another way to absorb the information in this video